
Ajaib.co.id – Matriks tak sekadar pelajaran siswa SMA, karena juga terdapat dan berguna dalam kehidupan kita sehari-hari. Asal muasalnya, ditemukan oleh Arthur Cayley (1821-1895), seorang ahli matematika dari Inggris yang sering berkutat dengan aljabar. Selain itu, ia juga membantu pendirian sekolah modern matematika murni di Inggris.
Pengertian dan Jenis-Jenisnya
Matriks disebut juga susunan bilangan yang disusun dalam baris dan kolom sehingga berbentuk persegi panjang. Matriks bisa berbentuk persegi dengan ukuran 2 x 2, 2 x 3, 3 x 3, 4 x 4, dan masih banyak lagi. Ini tidak berbeda dengan bilangan karena dapat dioperasikan dengan berbagai macam operasi seperti perkalian, penjumlahan, pengurangan dan transpose. Dengan menyusunnya, perhitungan bilangan dapat dilakukan lebih tersusun.
Di dunia matematika, matriks merupakan kumpulan bilangan, simbol, atau ekspresi, berbentuk persegi panjang yang disusun menurut baris dan kolom. Dalam penggunaannya, dapat dikalikan, dijumlahkan, dikurangkan dan diuraikan. Bilangan yang terdapat dalamnya disebut dengan istilah elemen atau anggota.
Sedangkan jenis dan sifat-sifat matriks setidaknya ada delapan, yaitu:
1. Nol: kumpulan bilangan yang semua elemennya bernilai nol.
2. baris Matriks: kumpulan elemen yang hanya terdiri satu baris saja.
3. Matriks Kolom: terdiri satu kolom saja.
4. Persegi: yang jumlah baris dan kolom sama.
5. Segitiga atas: kumpulan bilangan atau simbol secara persegi dengan elemen di bawah diagonal utamanya bernilai nol.
6. Segitiga bawah: kumpulan bilangan atau simbol secara persegi dengan elemen di atas diagonal utamanya bernilai nol.
7. Miagonal: kumpulan bilangan atau simbol secara persegi yang elemennya bernilai nol, kecuali pada diagonal utamanya tidak selalu nol.
8. Identitas: sekumpulan bilangan skalar dengan elemen pada diagonal utamanya bernilai satu.
Cara Mencari Determinan Matriks
Determinan merupakan nilai yang dihitung dari unsur-unsur matriks persegi. Matriks persegi memiliki banyak baris dan kolom yang sama, sehingga bentuknya terlihat seperti persegi. Cara menentukan determinan juga akan berbeda pada tiap ordonya.
1. Determinan Berordo 2 x 2
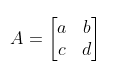
Matriks A memiliki ordo 2 × 2 dengan elemen matriks a dan d yang terletak pada diagonal utama. Sedangkan b dan c terletak pada diagonal kedua.
Nilai determinan A, disimbolkan dengan [A], merupakan bilangan yang diperoleh dengan cara mengurangkan hasil kali elemen-elemen pada diagonal utama dan hasil kali elemen-elemen diagonal kedua.
Rumus:
Det (A) = |A| = ad – bc
Contoh Soal Determinan Berordo 2 x 2
1. Tentukan determinan dari matriks berikut ini!

Solusi:
Jika kamu perhatikan matriks di atas, kamu bisa langsung menghitung nilai determinan dengan rumus yang telah diketahui.
Det (A) = |A| = ad – bc
|A| = (5 x 6) – (2 x 4)
|A| = 30 – 8
|A| = 22
2. Determinan Berordo 3 x 3
Matriks berordo 3×3 berbentuk persegi dengan banyak kolom dan baris sama yaitu tiga.

Untuk menghitung determinan berordo 3×3, kamu bisa menggunakan aturan Sarrus.

Contoh Soal Determinan Berordo 3×3
1. Tentukan determinan dari matriks di bawah ini!

Untuk menyelesaikan soal di atas, maka kamu bisa menggunakan aturan Sarrus.
|A| = aei + bfg + cdh – ceg – afh – bdi
|A| = (1x5x6) + (4x2x1) + (1x2x3) – (1x5x1) – (1x2x3) – (4x2x6)
|A| = 30 + 8 + 6 – 5 – 6 – 48
|A| = -15
Penggunaan di Luar Matematika
Seperti yang telah disinggung di atas, matriks bukan hanya pelajaran siswa SMA. Penggunaannya dibutuhkan dalam bidang yang lebih luas lagi, meski bidang tersebut tak jauh dari matematika.
Berikut ini penggunaannya dalam kehidupan sehari-hari:
1. Bidang ekonomi
Dapat memudahkan dalam membuat analisis masalah ekonomi beserta dengan input dan output-nya, tentunya dengan menetapkan variabel terlebih dahulu. Penelitian ekonomi pun tak lepas dari penggunaan ilmu ini.
2. Bidang matematika
Kamu bisa menggunakannya untuk menyelesaikan tugas atau studi kasus di bidang matematika. Misal memecahkan masalah persamaan linier, transformasi linear dari bentuk umum ke fungsi linear, serta memodifikasinya untuk kepentingan membuat tugas, penelitian, menyusun data, dan lainnya. Dengan menggunakan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur.
3. Untuk investigasi
Selain itu, dapat digunakan untuk investigasi laporan keuangan, penyimpangan administrasi, penyelidikan korupsi, dan masih banyak lagi.
4. Untuk perangkat lunak
Sebagai media edukasi, Microsoft Excel menerapkan prinsip matriks di dalam sistemnya, sehingga perangkat lunak ini dapat membantu perhitungan yang memiliki orde banyak. Perhitungannya pun lebih cepat dan efisien dibanding dengan menghitung manual. Selain itu, para guru dapat menggunakan rumus tersebut di Excel dalam pelajaran Akuntansi dan meminta siswa untuk menyelesaikannya.
5. Untuk pemrograman
Dapat digunakan untuk pemrograman membuat suatu sistem di pemerintahan atau korporasi, statistik, manajemen informatika, dan bidang lainnya.
Dengan mengetahui penggunaan tersebut, kamu bisa lebih memahami arti penting matriks. Tak ada salahnya juga kalau kamu mendalaminya. Karena lapangan pekerjaan yang bersinggungan dengan ilmu tersebut sangat terbuka lebar. Industri perbankan, keuangan, teknologi informasi, dan lainnya membutuhkan orang yang menguasainya.












